Transformation变换
Model Transform 模型变换
2D变换
Linear Transformation 线性变换
矩阵形式为
Scale Matrix 缩放
Reflection Matrix 镜像
Horizontal reflection:
Shear Matrix 切变
Horizontal shift:
Rotate 旋转
默认绕原点
推导:
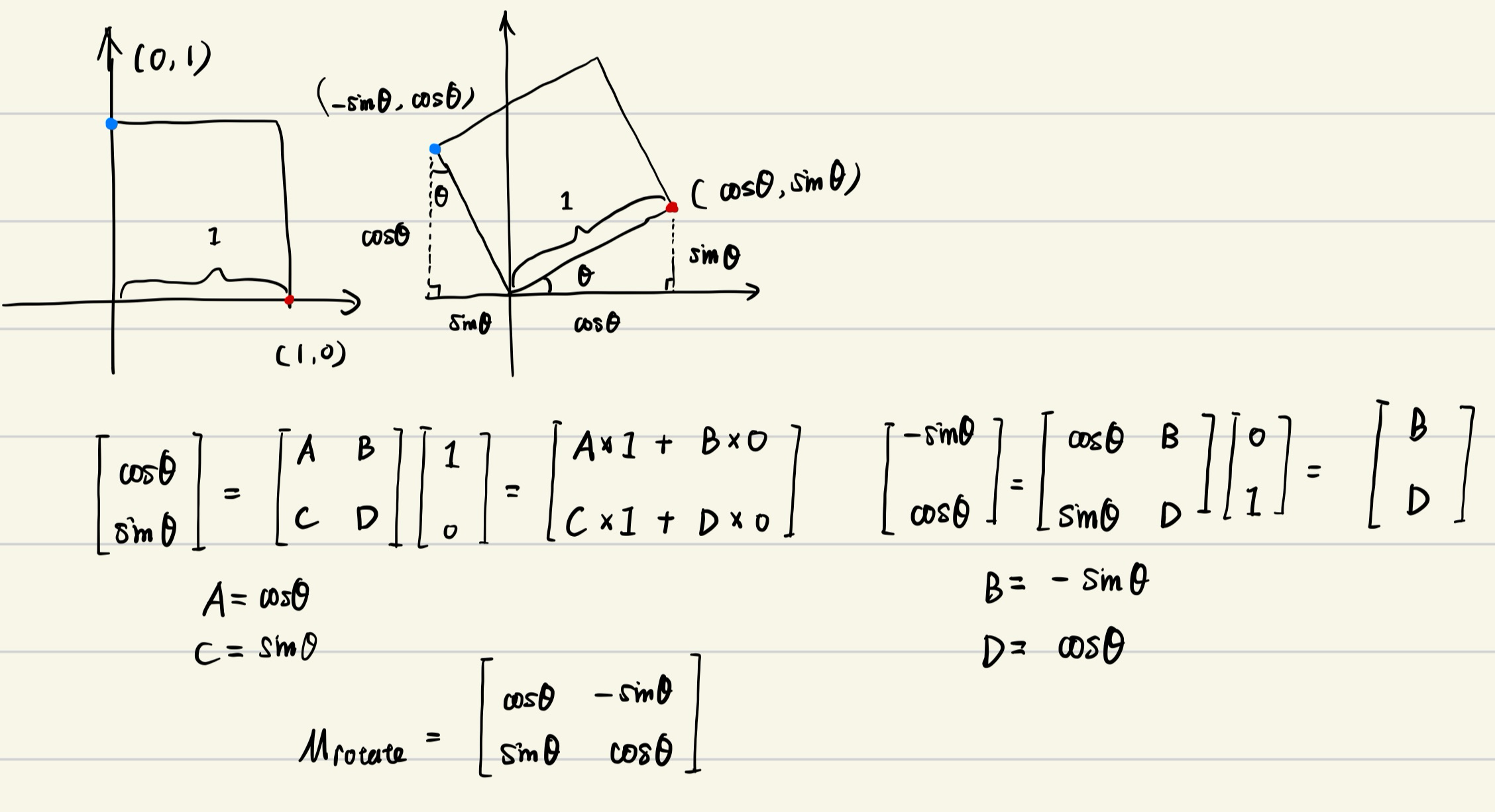
Translation 平移
这个变换无法直接写为统一的矩阵形式
因为平移不是线性变换
但是为了变换的形式的统一,可以引入齐次坐标(homogeneous coordinates)来表示
齐次坐标
对于二维向量,增加一个维度
2D Point =
2D Vector =
在矩阵运算时
同时,增加的维度在运算时也具有意义
对于
vector + vector = vector
point - point = vector
point + vector = point
point + point = ??
对于最后一种情况,得到的也是一个点,在进行标准化运算后,得到的是两点的中点
引入齐次坐标的目的是能够使用一个矩阵乘一个向量来表示所有变换
以上
用齐次坐标的形式来表示
Scale
Rotation
Translation
Inverse Transform 逆变换
逆矩阵
Composing Transform 组合变换
因为矩阵运算具有结合律,不同类型的变换可以通过多个矩阵相乘合成为一个变换矩阵。但需要注意矩阵运算不满足交换律,因此变换是具有顺序的,例如先旋转再平移、先平移再旋转可能会得到不同的结果。
在使用多个矩阵进行变换时,变换是从右向左应用的
例如
通过预先将多个矩阵变换合成为一个矩阵,可以在运算时提高性能
Decomposing Complex Transforms 分解变换
如何绕任意一个点进行旋转变换?
由于我们定义的旋转矩阵是绕原点进行旋转的,可以先将这个点移动到原点,进行旋转变换后,再进行一次平移还原到原来的位置。可表示为
旋转变换的一些性质
对于旋转矩阵
若旋转角度为
即旋转
由此可得
在数学中,如果一个矩阵的逆等于转置,称这个矩阵为正交矩阵
3D变换
3D Point =
3D Vector =
3D 仿射变换
应用这个矩阵时,先进行线性变换,再进行平移
Scale
Translation
Rotation(x-, y-,z- axis)
Euler angles 欧拉角
对三维空间中的旋转,可以用分别绕x,y,z轴的三个旋转组合而成
通常把三个分量称为roll,pitch,yaw
但是欧拉角旋转在两个轴重合时,会出现失去一个自由度的情况,称为万向节死锁
Rodrigues' Rotation Formula
绕任意轴
Quaternion 四元数旋转
能够应用于插值运算
留个坑详解四元数(未完成)
View Transform 观测变换
进行观测变换需要大量信息,包括:摄像机的位置和朝向、投影的类型、视场的大小( FOV field of view)、渲染的分辨率
通常可以把观测变换分解为三个流程
Camera Transform 相机变换
Projection Transform 投影变换
Viewport Transform 视口变换
在变换流程中坐标系统有特定的名称:
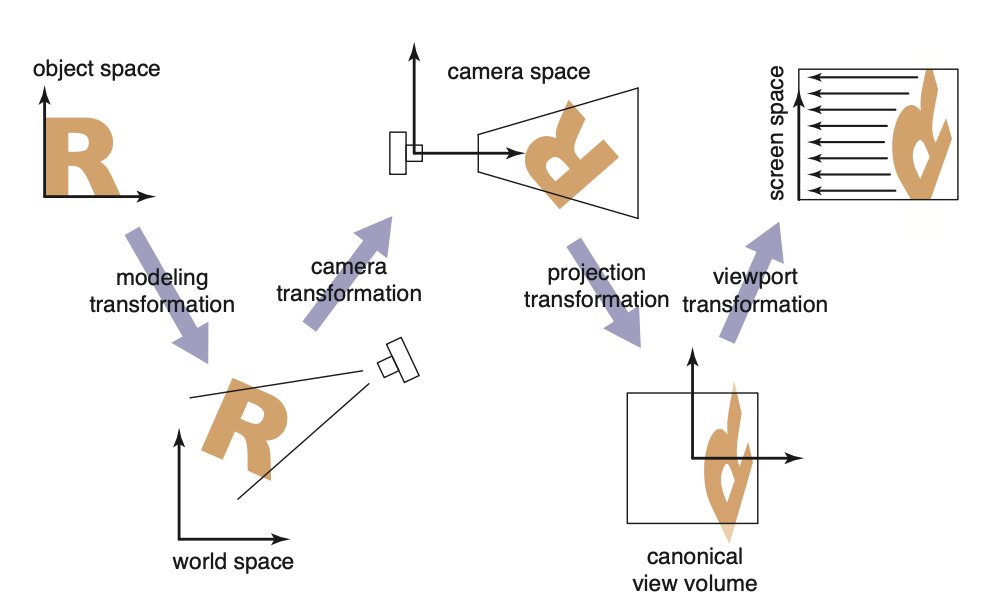
Figure 8.2 from Fundamentals of Computer Graphics, 5th Edition
一些别名
camera space也叫eye space,camera transformation也称作viewing transformation,canonical view volume也叫clip space或normalized device coordinates(NDC),screen space也叫pxiel coordinates
Fundamentals of Computer Graphics, 5th Edition P159
Camera Transform
相机变换将点转变为归一化坐标(canonical cooridnates)
定义一个相机变换:
Position
Look-at/gaze direction
Up direction
由于运动是相对的,为了简化相机变换,我们可以把摄像机相对物体的运动看做物体相对摄像机的运动。把摄像机固定在原点,up朝向
用变换来描述:
将摄像机移动到原点
把
把
把
写成矩阵形式
将摄像机的坐标轴旋转到
合并后得到
Viewport Trasnform 视口变换
将经过camera transform变换后得到的NDC坐标绘制到大小为
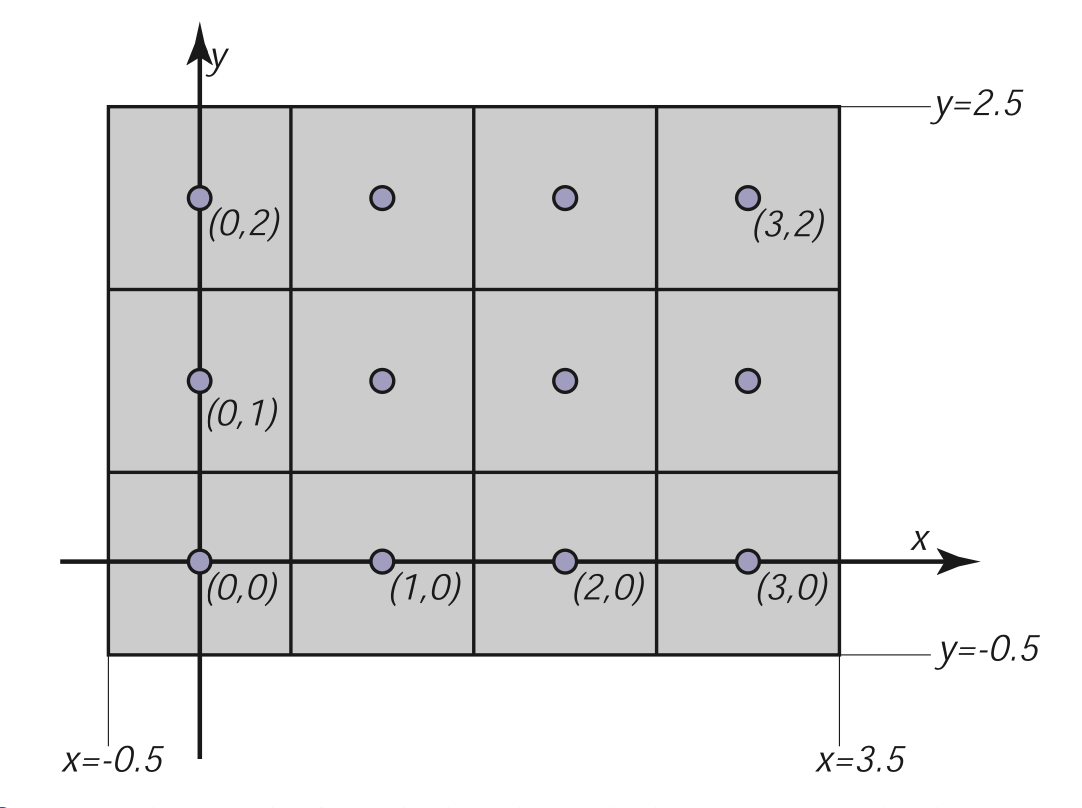
Figure 3.10 from Fundamentals of Computer Graphics, 5th Edition
写作矩阵形式:
此处暂时忽略了
Projection Transform 投影变换
Orthographic projection 正交投影
在空间中定义一个范围
在经过
Perspective Transform 透视变换
透视投影在空间中的范围称作Frustum
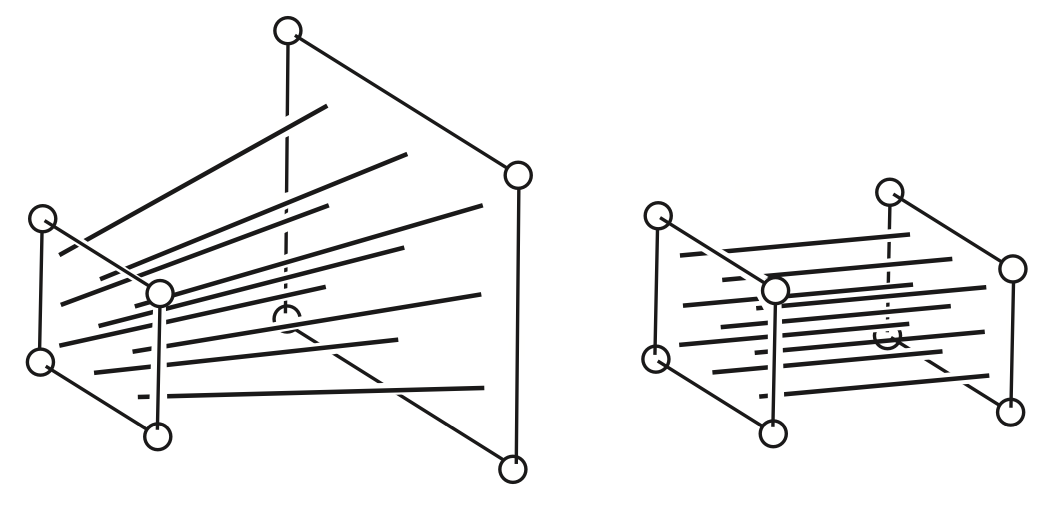
Figure 8.13 from Fundamentals of Computer Graphics, 5th Edition
通过侧视图,我们可以推导出在进行透视投影后,
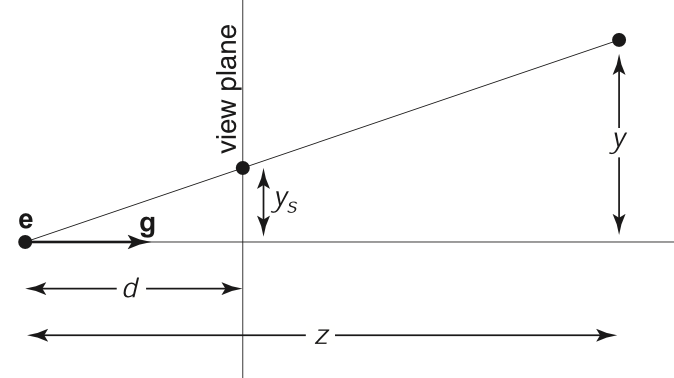
Figure 8.8 from Fundamentals of Computer Graphics, 5th Edition
但是我们可以对齐次坐标运算进行推广,来实现在仿射变换中使用除法
先前我们规定用
现在我们可以定义将
具体来说,线性变换允许我们实现
仿射变换将变换扩展为
将
这种变换可以称作线性有理函数,但是一个额外的约束条件是,坐标每个分量的分母都是相同的
将这些变换合并为一个矩阵
对于这个变换矩阵
Perspective Projection 透视投影
在透视投影中,我们将采用惯例,将摄像机放在原点,朝向
透视投影也可以分解为两个步骤,先将投影区域Frustum压缩成正交投影中的轴对齐的一个四方柱体,再进行正交投影
通过侧视图和俯视图,利用三角形相似进行推导,可以得到
将齐次除法还原,
再考虑一些特殊点:
近平面上的点在压缩后不会发生变化,
远平面上的点在压缩后
于是有方程组
最终我们得到
投影变换的流程
compute
compute
compute
将
参考资料
Fundamentals of Computer Graphics, 5th Edition
GAMES101 Lecture03-04